Startseite
Über Mich
AHP4
Galerie
Sehschlangen
 Tourenbuch
Bookmarks
Elektronik
Bewertung
Geschichten

Klausur Informatik I Ecker/Falkemeier WS97/98

Aufgabe:123456789Summe
max. Punkte108201210105520100

Aufgabe 1:

a)Wie lautet die mögliche Definition für eine binäre Relation?
b)Gib zwei mögliche Darstellungsformen von binären Relationen an.
c)Welche Eigenschaften hat eine Ordnungsrelation?
d)Wie lautet die Definition für einen endlichen Automaten?
e)Erläutere den Unterschied zwischen einem Eulerschen Zykel und einem Hamilton-Kreis.

Aufgabe 2:


Gegeben sei die folgende Nachricht:

BCCADBDDEACCCBBACCAEBECCCEBCEC

Gib die zugehörige Huffman-Kodierung an. Benutze dazu den in der Übung vorgegebenen Algorithmus.

Aufgabe 3:


Gegeben sei die Menge der Vorgänge: A = {A,B,C,D,E,F,G,H,I,J,K} mit den Zeitangaben:
t(A) = 5, t(B) = 2, t(C) = 1, t(D) = 3, t(E) = 1, t(F) = 4, t(G) = 2, t(H) = 6, t(I) = 5, t(J) = 1 und t(K) = 2

Folgende Präzedenzen liegen vor:

A<G, A<H, B<E, B<D, C<F, D<F, E<I, E<J, F<K, G<I, G<J, J<K

Zeichne den Netzplan und ermittle die frühestmögliche und spätestmögliche Zeit der einzelnen Ereignisse sowie sämtliche kritischen Pfade anhand der Critical Path Method (CPM).

Vorgänge ohne Vorgängervorgang sind: A, B und C.
Vorgänge ohne Nachfolgevorgang sind: H, I und K.

Hinweis:

Die frühestmögliche Zeit eines Ereignisses E = {1, ..., m} ist gegeben durch:
e(E) = 0 (für E = 1, (Anfangsereignis))
e(E) = max{e(E´) - t(A) | delta_null(A) = E und delta_eins(A) = E´}

Die spätestmögliche Zeit eines Ereignisses E erhält man durch die Ausnutzung von Wartemöglichkeiten:

l(E) = e(E) für E = m (Endereignis)
l(E) = min{l(E´) - t(A) | delta_null(A) = E und delta_eins(A) = E´}

Aufgabe 4:

Gegeben sei der folgende reguläre Ausdruck:

01(((10)*|111)*|0)*1

Gib den zugeörigen deterministischen endlichen Automaten an. Die Überführungsfunktion soll sowohl als Transitionsdiagramm, als auch als Matrix angegeben werden.

Aufgabe 5:

Gib den folgenden BOOLeschen Ausdruck in vollständiger konjunktiver Normalform an:

(x1 <=> x2) => x3

Zeichne ferner zu dem obigen Ausdruck die äquivalente Schaltung. Verwende nur die DIN-Schaltsymbole für UND, ODER und NICHT.

Aufgabe 6:

Zeichne zu folgendem Ausdruck ein Binary Decision Diagramm:

((x1 xor x4) => (x2 and x3)) <=> ((x2 <=> x4) or (x1 => x3))

Aufgabe 7:

Negiere folgenden Prädikatenlogischen Ausdruck:

für alle x.((x or (not y)) => (x and z)) => es existiert y.(y and (z => x))

Aufgabe 8:

Überprüfe mit Hilfe des Resolutionsverfahrens, ob folgender Ausdruck eine Tautologie ist:

((A => B) or (B and D)) => (D or ((not A) and C))

Aufgabe 9:

Bestimme den kürzesten Weg von A nach G in folgendem Graphen mit dem Verfahren von Dijkstra: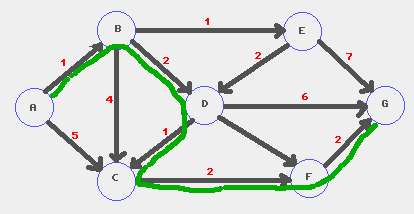
Graph

Lösungen

Aufgabe 1:

a)Eine binäre Relation ist definiert als
R enthalten im Kartesischen Produkt S1xS2, S1 und S2 sind Mengen.
b)1. Wertetabelle
2. Matrix
c)Eine Ordnungsrelation ist reflexiv, transitiv und antisymmetrisch.
d)Ein endlicher Automat ist definiert als Quintupel (Q, Sigma, delta, q0, F)
wobei
  • Q = endliche Menge von Zuständen des Automaten
  • sigma = Ein Alphabet über eine endliche Menge von Zeichen
  • delta = Transitionsfunktion. delta ist enthalten in QxSigma
    Bei totalen Automaten muß delta eine totale Funktion sein
  • q0 aus Q ist der Startzustand
  • F enthalten in Q ist eine endliche Menge von Endzuständen
e)
Eulerscher Zykel : Gesucht ist ein Kreis, der in einem Knoten beginnt und endet und dabei jeden Bogen genau einmal benutzt.
Hamilton-Kreis : Gesucht ist ein Weg,der im selben Knoten beginnt und endet und jeden Knoten genau einmal durchläuft.

Aufgabe 2

Das Alphabet Sigma ist {A, B, C, D, E }
Für jedes Zeichen aus Sigma muß nun die Wahrscheinlichkeit ermittelt werden. Die Anzahl der Zeichen in der Nachricht beträgt n = 30.
pA4/30
pB6/30
pC12/30
pD3/30
pE5/30
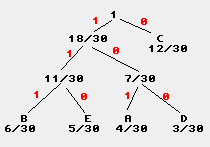
Mit den jetzt bekannten Wahrscheinlichkeiten läßt sich der Huffman-Baum erstellen. Die Äste werden mit Binärziffern beschriftet, rechte Teiläste erhalten eine 0, linke eine 1. Die Codes erhält man, indem man von der Wurzel bis zu den Blättern hinabsteigt und dabei die Binärziffern mitschreibt.


Es ergibt sich dann folgende Code-Tabelle:
ZeichenCodeLänge
A1013
B1113
C01
D1003
E1103

Aufgabe 3:

Der Netzgraph hat folgende Gestalt:
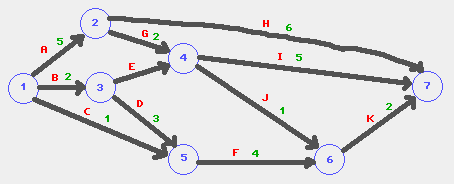
Netzplan

Die Kanten wurden mit dem Vorgang und der dazugehörigen Zeit farbig hervorgehoben beschriftet.
Mit diesem Graphen läszlig;t sich nun die Tabelle für l(E) und e(e) und den Pufferzeiten l(E) - e(E) berechnen:
A1234567
e(E)05275912
l(E)053761012
l(E) - e(E)0010110
Der kritische Pfad wählt die Knoten, die die Pufferzeit 0 besitzen. Es ergibt sich also als kritischer Pfad 1, 2, 4, 7.

Aufgabe 4

Sigma = {0, 1 }.
Es ergibt sich für den genannten regulären Ausdruck ein Automat mit folgendem Transisitionsdiagramm und mit folgender Transitionsmatrix:
Um einen total definierten Automaten zu erhalten, muß man einen Fehlerzustand q5 mit Trap einführen.

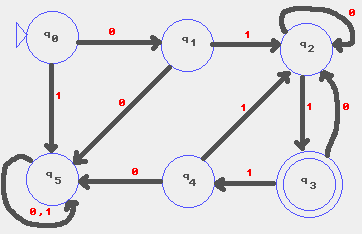
Automat

Transitionsmatrix:
Delta01
q0q1q5
q1q5q2
q2q2q3
q3q2q4
q4q5q2
q5q5q5

Aufgabe 5

E = (x1 <=> x2) => x3
Wahrheitstabelle :
x1 x2 x3 x1 <=> x2 E
00010
00111
01001
01101
10001
10101
11010
11111
Es ergibt sich für die KNF:
E = (x1 v x2 v x3) AND ( (NOT x1) v (NOT x2) v x3)
Daraus resultiert folgende Schaltung:
KNF

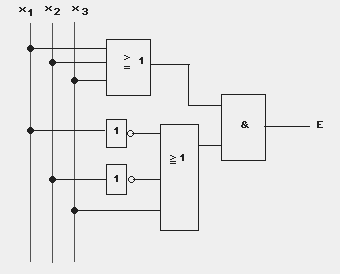
Aufgabe 7


Letzte Änderung : 22-Aug-2023
Copyright Jens Köhler, Wolfsburg, Obere Dorfstraße 10d